α卤有机化合物的结构性质,自然键轨道,理论泛函计算(DFT)和能量
吉达市Seidy1*以及Shahriar ghhamamy1
DOI:http://dx.doi.org/10.12944/CWE.7.2.05
摘要
本文讨论了C3.H2F4Br2采用基于lanl2dz基集的DFT (B3LYP)方法进行计算。B3LYP/ lanl2dz2计算结果表明,C3.H2F4Br2.
关键字
晕氟烷烃,C3H2F4Br2,电子结构,计算,振动分析,B3LYP水平
复制以下内容以引用本文:
Seidy N, ghhamamy S.结构性质,自然键轨道,理论泛函计算(DFT)和α半有机化合物的能量。全球环境研究2012;7(2):221-226 DOI:http://dx.doi.org/10.12944/CWE.7.2.05
复制以下内容以引用此URL:
Seidy N, ghhamamy S.结构性质,自然键轨道,理论泛函计算(DFT)和α半有机化合物的能量。环境科学学报,2012;7(2):221-226。可以从://www.a-i-l-s-a.com/?p=2779
文章发布历史
| 收到: | 2012-07-12 |
|---|---|
| 接受: | 2012-09-17 |
简介
有机卤烷化合物或卤碳化合物是其中一个或多个碳原子与一个或多个卤原子(氟、氯、溴或碘- 17族)以共价键相连的化学物质,从而形成有机氟化合物、有机氯化合物、有机溴化合物和有机碘化合物。氯卤烃是最常见的,被称为有机氯化物。许多人工合成的有机化合物,如塑料聚合物和一些天然化合物,都含有卤素原子;它们被称为卤化化合物或有机卤素。有机氯化物是工业上最常用的有机卤化物,尽管其他有机卤化物通常用于有机合成。除了极其罕见的情况,有机卤化物不是由生物产生的,但许多药物都是有机卤化物。有机卤素化合物在理论和工业上有着广泛的应用[1-4]。卤代烃的常用用途包括溶剂、杀虫剂、制冷剂、耐火油、弹性体、粘合剂和密封剂的成分、电绝缘涂料、增塑剂和塑料。许多卤碳化合物在工业上有专门用途。一种卤素,三氯蔗糖,是一种甜味剂。 Many different data have been found about the structural properties of halo compounds, but they are insufficient and opposing in somewhere.The investigation of the structures and properties of the compound and similarities are interested. The structure has been confirmed by neutron diffraction studies and is justified by VSEPR theory [5-8]. During this study we report the optimized geometries, assignments and electronic structure calculations for the compound. The structure of the compound has been optimized by using the DFT (B3LYP) method with the LANL2DZbasis sets, using the Gaussian 09 program [9]. The comparison between theory and experiment is made. Density functional theorymethods were employed to determine the optimized structures of C3H2F4Br2and Initial calculations were performed at the DFT level and split- valence plus polarization LANL2DZbasis sets were used. Local minima were obtained by full geometrical optimization have all positive frequencies [10].
方法
所有计算均采用高斯09程序[11]进行。将优化后的结构参数用于高频和DFT水平的振动频率计算,并将所有静止点表征为最小值。谐波振动频率(ν),单位为厘米-1所有化合物的红外强度(int)在各自充分优化的几何图形上的相同水平上进行。能量最小的分子几何是通过能量最小来定位的,相对于所有几何坐标,不施加任何对称约束。
结果 和讨论 分子性质
化合物结构如图1所示。所有的计算都是用计算机程序高斯09进行的。通过优化几何结构(表1)确定了化合物的键和角的理论计算。表1中的NBO分析和表2中的NBO计算杂化。我们无法将给出的键长和键角值的计算结果与实验数据进行比较。因为目前还没有标题化合物的晶体结构。B3LYP/ lanl2dzd计算结果表明,(C1- f6) C3H2F4Br2和化合物1-2的键长分别为1.3909 Å和1.3765 Å。和(C- br -)键长值3.H2F4Br2化合物1-2分别为1.8031Åand 1.7727Å。卤代烃化合物大多是不溶于水的致密液体和固体。卤素的电负性都比碳强,这使得碳卤素键是一个极性键,碳端有一个轻微的正电荷(d +)
这个键和卤素端带一个轻微的负电荷(d-)。
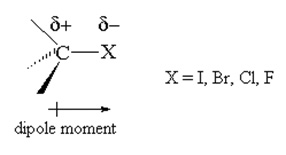
碳-卤键强度依次为C-F > C-Cl > C-Br > C-I氟化烃的反应性往往低于其他烷基卤化物,这主要是由于C-F键强度较高。
结构的NBO研究
自然键轨道(NBOs)是一种局部化的少中心轨道,它描述了电子对以最优紧致形式形成的路易斯样分子键模式。更确切地说,nbo是一组标准正交的局部“最大占用”轨道,其引导N/2个成员(或N开壳情况下的成员)给出了最准确的可能的刘易斯式描述N电子密度。这一分析是通过检查“填充”(供体)lewis型NBOs和“空”(受体)非lewis型NBOs之间所有可能的相互作用进行的,并通过二阶摄动理论估计它们的能量重要性。由于这些相互作用导致从理想化的Lewis结构的局域nbo到空的非Lewis轨道的占用(因此,偏离了理想化的Lewis结构描述),它们被称为对零阶自然Lewis结构的“离域”修正。利用高斯09中实现的自然键轨道(NBO)模块计算了自然电荷。NBO计算杂化是我们研究的重要参数。这些数量来自NBO总体分析。前者提供了一个更接近经典刘易斯结构的轨道图像。涉及所选键杂化的NBO分析采用B3LYP方法和LANL2DZ理论水平计算(表2)。
这些数据表明配体原子与中心金属原子之间的电子超共轭。这些共轭是建立在p-d π键基础上的。NBO计算了C的杂化3.H2F4Br2表明所有配合物都有SPX杂化和非平面构型。这些分子的总杂化是SPX这已经得到了结构方面的证实。键杂化量显示中心原子角不等(表2)显示了八面体和VSEPR结构的扭曲,并证实了VSEPR结构的偏差。在C3H2F4Br2孤对位于溴原子上,C-F键杂化轨道明显离域。的确,在相互作用中能量从电荷转移到sc3.H2F4Br2复合体证实了上述观点,并在C的平均值3.H2F4Br2预测了最大相互作用能(表3)。
前沿分子轨道
最高已占分子轨道(HOMO)和最低未占分子轨道(LUMO)是参与化学稳定的主要轨道。HOMO代表捐赠电子的能力,LUMO作为电子受体代表获得电子的能力。采用B3LYP/LANL2DZ方法[12]计算HOMO和LUMO能量。这种电子吸收对应于从基态到第一激发态的跃迁,主要由最高占据的分子或轨道(LUMO)的一个电子激发来描述。因此,HOMO的能量与电离势直接相关,而LUMO的能量与电子亲和能直接相关。HOMO轨道和LUMO轨道之间的能量差称为能隙,能隙是结构稳定性的重要指标。此外,图2显示了最高已占分子轨道(HOMOs)和最低未占分子轨道(LUMOs)的三维图。在LANL2DZ上也计算了HOMO-LUMO能量,其数值分别列在图2中。
结论
在本研究中,我们对两种有兴趣的晕有机化合物进行了理论研究。本文采用基于lanl2dz基集的DFT (B3LYP)方法,计算了静止点和最小能量路径的优化几何形状和频率。B3LYP/LANL2DZ计算结果表明,C3.H2F4Br2.
确认
我们非常感谢伊玛目霍梅尼国际大学研究委员会的资助,资助号为751387-91。
参考文献
有机卤烷化合物或卤碳化合物是其中一个或多个碳原子与一个或多个卤原子(氟、氯、溴或碘- 17族)以共价键相连的化学物质,从而形成有机氟化合物、有机氯化合物、有机溴化合物和有机碘化合物。氯卤烃是最常见的,被称为有机氯化物。许多人工合成的有机化合物,如塑料聚合物和一些天然化合物,都含有卤素原子;它们被称为卤化化合物或有机卤素。有机氯化物是工业上最常用的有机卤化物,尽管其他有机卤化物通常用于有机合成。除了极其罕见的情况,有机卤化物不是由生物产生的,但许多药物都是有机卤化物。有机卤素化合物在理论和工业上有着广泛的应用[1-4]。卤代烃的常用用途包括溶剂、杀虫剂、制冷剂、耐火油、弹性体、粘合剂和密封剂的成分、电绝缘涂料、增塑剂和塑料。许多卤碳化合物在工业上有专门用途。一种卤素,三氯蔗糖,是一种甜味剂。 Many different data have been found about the structural properties of halo compounds, but they are insufficient and opposing in somewhere.The investigation of the structures and properties of the compound and similarities are interested. The structure has been confirmed by neutron diffraction studies and is justified by VSEPR theory [5-8]. During this study we report the optimized geometries, assignments and electronic structure calculations for the compound. The structure of the compound has been optimized by using the DFT (B3LYP) method with the LANL2DZbasis sets, using the Gaussian 09 program [9]. The comparison between theory and experiment is made. Density functional theorymethods were employed to determine the optimized structures of C3H2F4Br2and Initial calculations were performed at the DFT level and split- valence plus polarization LANL2DZbasis sets were used. Local minima were obtained by full geometrical optimization have all positive frequencies [10].
方法
所有计算均采用高斯09程序[11]进行。将优化后的结构参数用于高频和DFT水平的振动频率计算,并将所有静止点表征为最小值。谐波振动频率(ν),单位为厘米-1所有化合物的红外强度(int)在各自充分优化的几何图形上的相同水平上进行。能量最小的分子几何是通过能量最小来定位的,相对于所有几何坐标,不施加任何对称约束。
结果 和讨论 分子性质
化合物结构如图1所示。所有的计算都是用计算机程序高斯09进行的。通过优化几何结构(表1)确定了化合物的键和角的理论计算。表1中的NBO分析和表2中的NBO计算杂化。我们无法将给出的键长和键角值的计算结果与实验数据进行比较。因为目前还没有标题化合物的晶体结构。B3LYP/ lanl2dzd计算结果表明,(C1- f6) C3H2F4Br2和化合物1-2的键长分别为1.3909 Å和1.3765 Å。和(C- br -)键长值3.H2F4Br2化合物1-2分别为1.8031Åand 1.7727Å。卤代烃化合物大多是不溶于水的致密液体和固体。卤素的电负性都比碳强,这使得碳卤素键是一个极性键,碳端有一个轻微的正电荷(d +)
这个键和卤素端带一个轻微的负电荷(d-)。
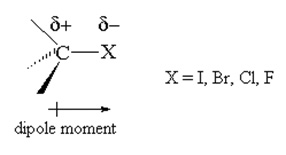
碳-卤键强度依次为C-F > C-Cl > C-Br > C-I氟化烃的反应性往往低于其他烷基卤化物,这主要是由于C-F键强度较高。
 |
表1:C3H2F4Br2一些选定键长(Å)和角度(°C)优化的几何参数 点击这里查看表格 |
结构的NBO研究
自然键轨道(NBOs)是一种局部化的少中心轨道,它描述了电子对以最优紧致形式形成的路易斯样分子键模式。更确切地说,nbo是一组标准正交的局部“最大占用”轨道,其引导N/2个成员(或N开壳情况下的成员)给出了最准确的可能的刘易斯式描述N电子密度。这一分析是通过检查“填充”(供体)lewis型NBOs和“空”(受体)非lewis型NBOs之间所有可能的相互作用进行的,并通过二阶摄动理论估计它们的能量重要性。由于这些相互作用导致从理想化的Lewis结构的局域nbo到空的非Lewis轨道的占用(因此,偏离了理想化的Lewis结构描述),它们被称为对零阶自然Lewis结构的“离域”修正。利用高斯09中实现的自然键轨道(NBO)模块计算了自然电荷。NBO计算杂化是我们研究的重要参数。这些数量来自NBO总体分析。前者提供了一个更接近经典刘易斯结构的轨道图像。涉及所选键杂化的NBO分析采用B3LYP方法和LANL2DZ理论水平计算(表2)。
 |
表2:NBO计算杂化 (B3LYP / LANL2DZ C3H2F4Br2) 点击这里查看表格 |
 |
表3 NBO基下Fock矩阵的二阶摄动理论分析(1)C3H2F4Br2 (2))a超共轭相互作用的平均能量(稳定能);b供体和受体的能量差i和j的NBO轨道;c F(i, j)是i和jnbo之间的福克矩阵元素 点击这里查看表格 |
 |
图1:C3H2F4Br2结构示意图 点击此处查看图 |
 |
图2:前沿分子的原子轨道 C3H2F4Br2 B3LYP/6-311理论轨道 点击此处查看图 |
这些数据表明配体原子与中心金属原子之间的电子超共轭。这些共轭是建立在p-d π键基础上的。NBO计算了C的杂化3.H2F4Br2表明所有配合物都有SPX杂化和非平面构型。这些分子的总杂化是SPX这已经得到了结构方面的证实。键杂化量显示中心原子角不等(表2)显示了八面体和VSEPR结构的扭曲,并证实了VSEPR结构的偏差。在C3H2F4Br2孤对位于溴原子上,C-F键杂化轨道明显离域。的确,在相互作用中能量从电荷转移到sc3.H2F4Br2复合体证实了上述观点,并在C的平均值3.H2F4Br2预测了最大相互作用能(表3)。
前沿分子轨道
最高已占分子轨道(HOMO)和最低未占分子轨道(LUMO)是参与化学稳定的主要轨道。HOMO代表捐赠电子的能力,LUMO作为电子受体代表获得电子的能力。采用B3LYP/LANL2DZ方法[12]计算HOMO和LUMO能量。这种电子吸收对应于从基态到第一激发态的跃迁,主要由最高占据的分子或轨道(LUMO)的一个电子激发来描述。因此,HOMO的能量与电离势直接相关,而LUMO的能量与电子亲和能直接相关。HOMO轨道和LUMO轨道之间的能量差称为能隙,能隙是结构稳定性的重要指标。此外,图2显示了最高已占分子轨道(HOMOs)和最低未占分子轨道(LUMOs)的三维图。在LANL2DZ上也计算了HOMO-LUMO能量,其数值分别列在图2中。
结论
在本研究中,我们对两种有兴趣的晕有机化合物进行了理论研究。本文采用基于lanl2dz基集的DFT (B3LYP)方法,计算了静止点和最小能量路径的优化几何形状和频率。B3LYP/LANL2DZ计算结果表明,C3.H2F4Br2.
确认
我们非常感谢伊玛目霍梅尼国际大学研究委员会的资助,资助号为751387-91。
参考文献
- ghhamamy, Sh., Z. Anvarnia, M. Jafari, K. Mehrani, H. Tavakol, Z. Javanshir和G. Rezaeibehbahani, 2009。两种新的碘晕配合物的合成与表征4H9)4N(我2Br)-和(C4H9)4N(我2Br)-以及它们结构的理论计算。主要基团化学,8: 299 - 306。http://dx.doi.org/10.1080/10241220903377481
- 贝克,1993,密度-功能热化学。3精确交换的作用。j .化学。理论物理,98: 5648 - 5652。http://dx.doi.org/10.1063/1.464913
- 孙达拉甘纳森,n.s Ilakiamani, 2007。用从头算和密度泛函理论分析3,4 -二甲基苯甲醛结构的振动光谱研究。光谱化学学报A辑,68: 680 - 687。http://dx.doi.org/10.1016/j.saa.2006.12.046
- 路易斯,D. F. V.约阿尼德斯和D. V.帕克,1994。一系列丁腈与醇诱导P450异构体的相互作用:构效关系的计算机分析。Xenobiotica,24: 401 - 408。http://dx.doi.org/10.3109/00498259409043243
- 拉尔夫,1992。化学硬度和电子化学势chimica学报,198: 781 - 786。
- 弗莱明,1976。前沿轨道和有机化学反应,威利,伦敦,第125页。
- 张伟,柯伦,2006。氟的合成应用。四面体62: 11837 - 11865。http://dx.doi.org/10.1016/j.tet.2006.08.051
- 王宏、乔永明、王宏,2005。Coucouvanis D, Koutmos M, Sturhahn W, Alp EA,赵j, Kramer SP FeCl4-和Fe2S2Cl42-的振动穆斯堡尔光谱、共振拉曼光谱和FT-IR光谱法模分析。Inorg。化学,44: 5562 - 5570。http://dx.doi.org/10.1021/ic0482584
- Vrajmasu, V. V., E. Mu¨nck,和E. L. Bominaar, 2004。四硫代铁(II)配合物Jahn - Teller畸变的理论分析.Inorg。化学,43: 4862 - 4866。http://dx.doi.org/10.1021/ic0400484
- ghhamamy, Sh., K. Mehrani, S. Rostamzadehmansor和H. Sahebalzamani, 2011。密度泛函理论研究了三种新型四卤代甲酸(III)配合物的结构和振动谱。自然科学,3., 683 - 688。http://dx.doi.org/10.4236/ns.2011.38091
- 弗里施,M. J.卡车,G. W. 1998。GASSIAN 98 (Revision A. 3)









